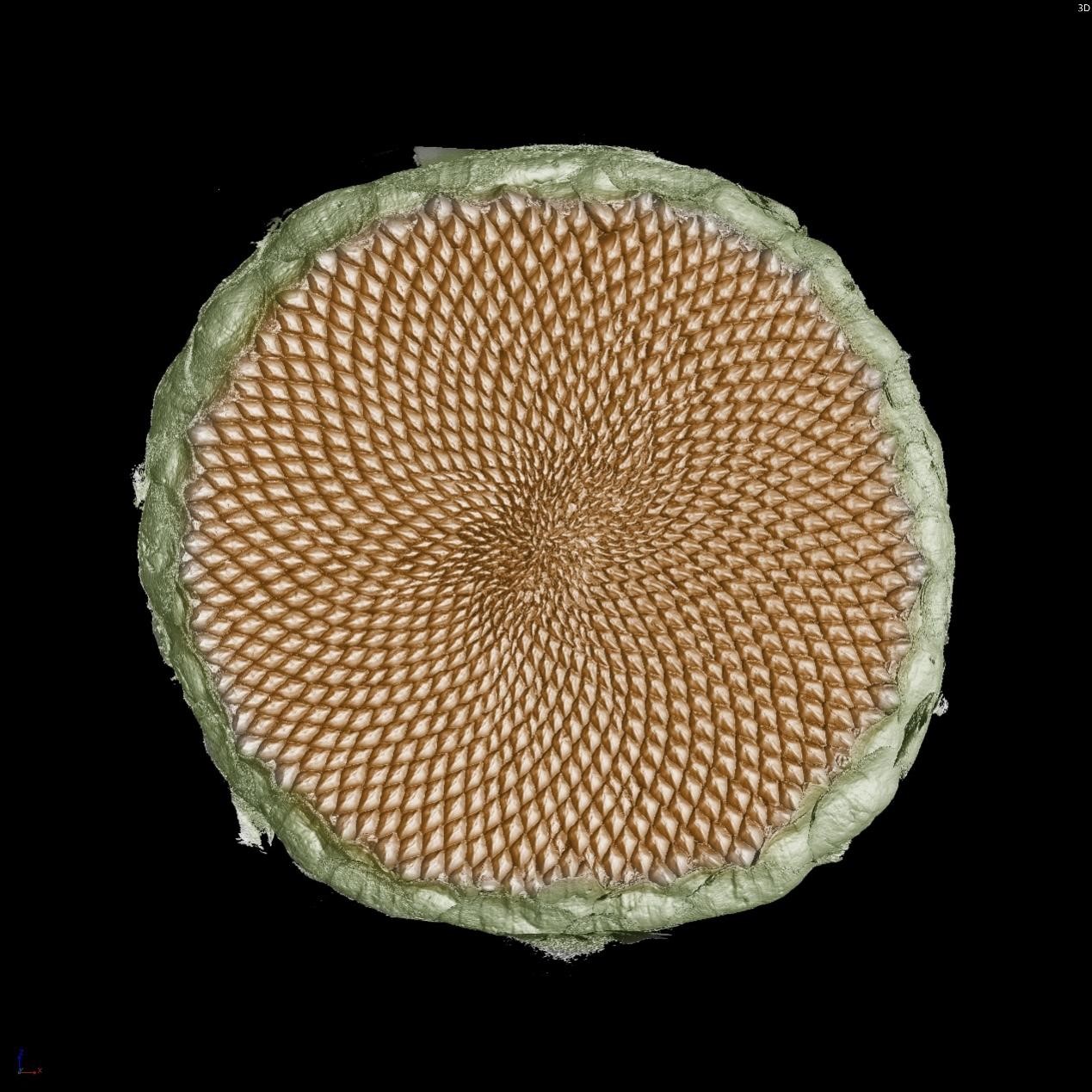
先来一张CT扫描的向日葵三维模型图，是不是感觉葵花种子的排列非常的紧密而有规律呢？向日葵圆盘的种子按照一定的发散角螺旋排列使得种子之间没有间隙，空间得到充分利用，这其中便蕴含着数学奥秘。

    在讲向日葵的数学之美前，先请大家复习两个数学概念，

    一个叫斐波那契数列，也叫兔子数列，它是这样的：

    1、1、2、3、5、8、13、21、34、55、89、144……

    还记得数学课上是怎么讲的吗？对，数列中每项是它前两项的和。

    第二个概念叫黄金分割，即0.618，

    请仔细观察兔子数列，如果用前一项除以后一项，即：

    1÷1=1

    1÷2=0.5

    2÷3=0.666…

    3÷5=0.6

    5÷8=0.625

    ……

    55÷89=0.617977…

    ……

    144÷233=0.618025…

    ……

    46368÷75025=0.6180339886…

    ……

    不难发现，数字越大，得到的结果越接近一个数字，即 0.618，这个数字就是“ 黄金分割”。

    向日葵种子的排列方式就是这种典型的数学模式，如下图：

    图中存在顺时针的螺线与逆时针的螺线，由于花盘螺线过密，我们间隔多行进行螺线勾勒。下图单独提取螺旋线，有发现什么规律吗？

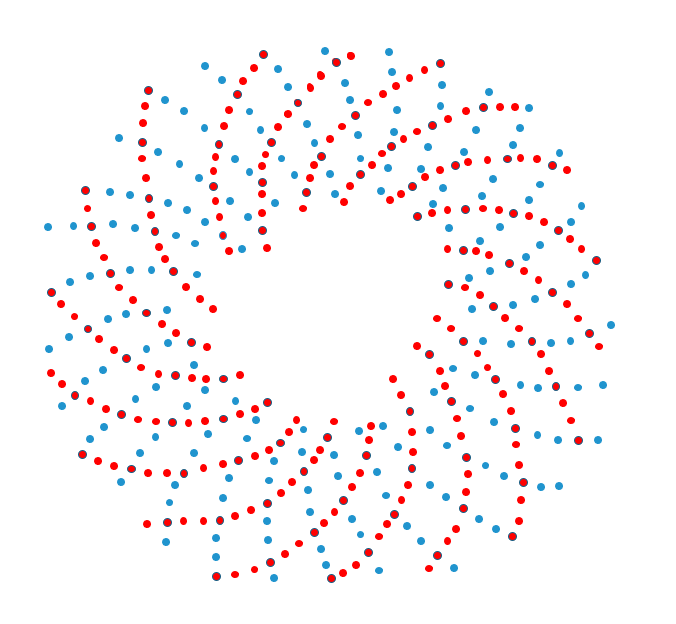
    那让我们分别来看看螺旋线吧，顺时针的红色螺线共有55条，是斐波那契数列其中一项。

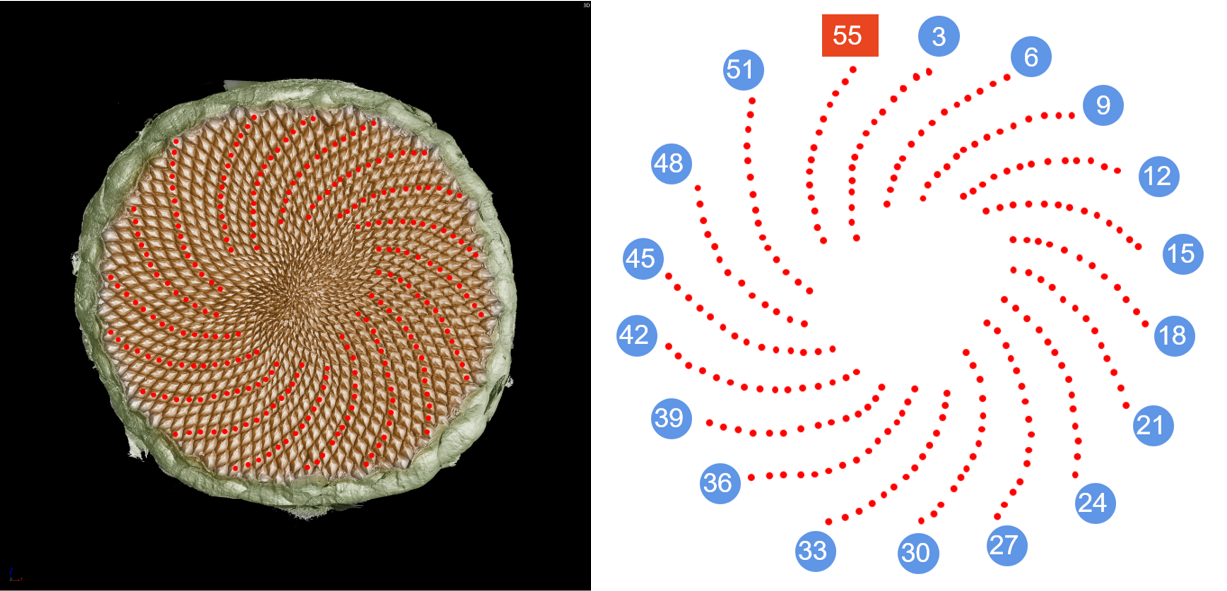
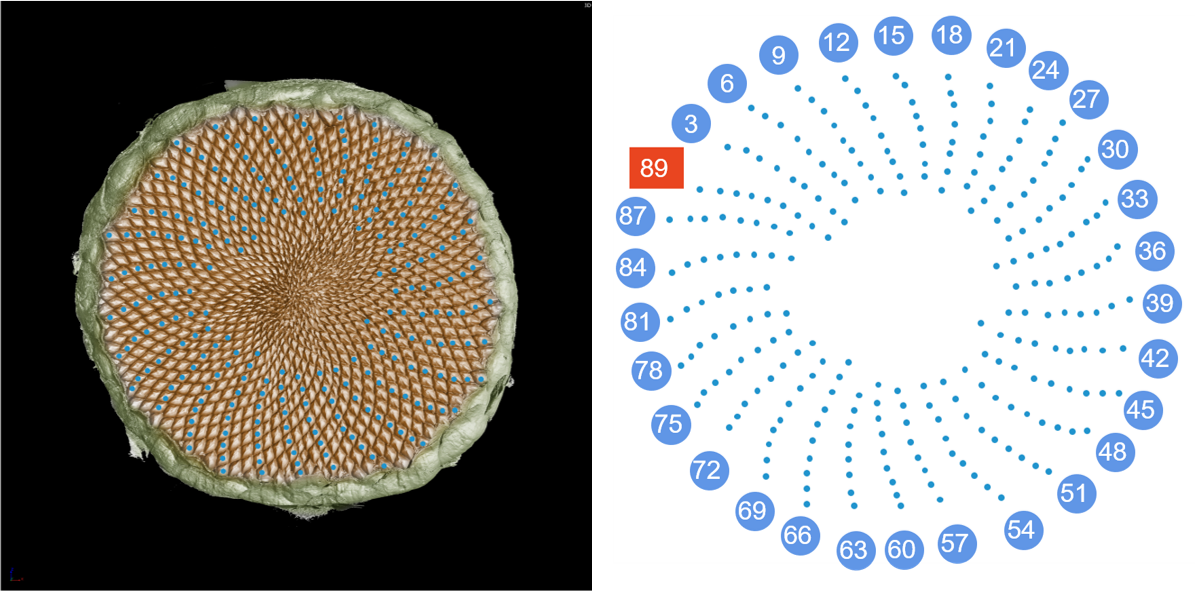
     接下来是逆时针的蓝色螺线共有89条，（55，89）正是斐波那契数列中相邻的两项。在向日葵的花盘中，普遍存在着斐波那契数列，较大向日葵的逆顺螺线数目可以是（89，144），更大的甚至可以达到（144，233）。

    对于向日葵来说，在有限的空间里开出足够多的花并结出足够多的种子是要务，在漫长的进化过程中，自然选择让向日葵有了可以用斐波那契数列和黄金分割来解释的数学之美。

    大自然的选择机制使得向日葵原基的生长遵循着有效率堆排的几何原理。一九七九年，数学家伏格（H. Vogel）以电脑模拟原基的生长情形，他用圆点来代表向日葵的原基，在发散角为固定值的假设下，试图找出发散角使这些圆点尽可能紧密地排在一起。实验证明，当发散角小于137.5°或大于超过 137.5°，圆点间都会出现空隙，只以一组螺线陈列。而发散角等于137.5°时，清晰的正反两组螺线叠加出现了，如果要使圆点排列没有空隙，发散角就必须是黄金角（137.5°为黄金角，是因为（360°-137.5°）/360°=0.618），只有这样，向日葵花盘最密实、坚固，能量吸收有效率。如下图，实际的生长顺序并不是距离临近的，而是按照“黄金角”的规律进行的。

    除了向日葵，自然界中随处可见斐波那契数列的踪迹。树枝上的分枝、花的瓣数都是斐波那契数列，桃梅杏李5，桔梗常为8，金盏花13等等。